FIND研究員:楊秉哲 
基於個資與資安疑慮,目前金融機構資料若要彼此共享,必須事先取得每一個使用者同意,對於擁有龐大用戶的金融機構而言,在人力及成本上均不堪負荷。國內基於個人資料保護法以及金融機構間共享指引之規範,目前仍需要使用者同意;然而,在國外已有相關案例,即運用安全多方計算與全同態加密技術,不需要取得使用者同意,即可進行資料共享,達到金融機構跨集團行銷之目的。
由百萬富翁問題衍生的安全多方計算
所謂的安全多方計算是一種密碼學技術,於1982年由科學家姚期智提出,其原型是來自「百萬富翁問題」,此問題描述如下:有兩個富翁,分別為甲和乙。他們各自知道自己的財產數字,且財產介於百萬至千萬等級,但甲和乙不知道對方的財產數字;他們在一次見面時,雙方都想知道到底誰的數更大一些。在這個場景內有幾個前提:一、兩人都不會說謊,所以這個場景中不存在造假之狀況;二、甲乙兩人皆希望能如實地比較出結果;三、兩人都希望知道對方財產的確切數字。安全多方計算的基礎版本設定是,甲乙雙方各自有一個對方看不見內容物的盒子,如果一百萬代表一瓶水,兩人在對方看不到對方的前提下,把對應財產數字的水瓶放入盒子,再同時把盒子放到天平上,這樣就可以透過天平偏向哪一方確認誰的財產比較多。安全多方計算的衍生版本有很多種,上面的例子僅能確認是否的答案,以下就最具代表性之「混淆電路」(Garbled Circuits, GC)作一說明。
混淆電路與不經意傳輸
我們同樣以百萬富翁問題甲與乙比誰的財產多為例,甲將先將同樣鎖頭的10個盒子依序貼上1至10號的貼紙,1代表100萬,10代表1000萬,接著假設甲有600萬,那麼代表100萬至500萬的1到5號盒子,會放入紅色卡片;代表600萬的6號盒子會放入綠色卡片;代表700萬至1000萬的7到10號盒子會放入藍色卡片。甲將卡片放完後,將盒子上鎖且放在一房間後離開,讓乙進來房間。乙依照自己的對應財產數從貼上貼紙的盒子作選擇。假設乙選擇7號盒,已將7號盒也加上一道自己才能解開的鎖,並所有盒子貼紙移除,並且銷毀其它9個盒子,再請甲進來房間,雙方拿出鑰匙解鎖,此時甲看到箱子裡面的藍色卡片,就知道乙的財產比他多,但由於甲也不知道乙選了幾號箱子,所以甲不會知道乙確切財產是多少。在這個場景下甲就可以在不知道乙財產前提下確認答案。此傳輸方式稱為不經意傳輸(Oblivious Transfer)。
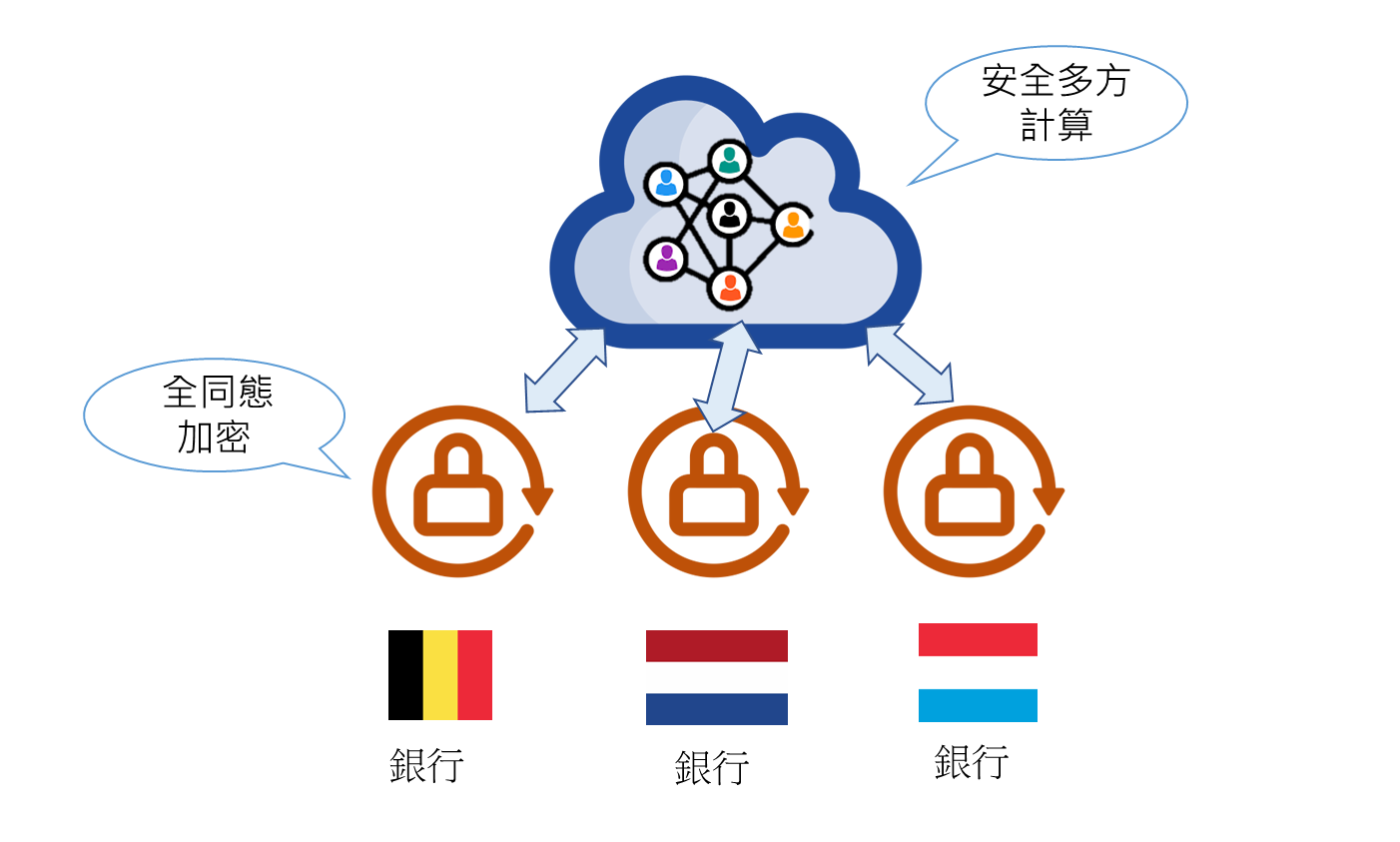
資料來源:作者自行繪製
圖1、銀行使用全同態加密與安全多方計算進行資料共享
應用現況與產業趨勢說明
多方安全計算目前已實際投入商業運用。例如:金融科技業者Inpher曾協助位於比利時的一間歐盟銀行,協助將其荷蘭、盧森堡一同銀行集團之資料跨境方式共享至比利時。原本比利時分行的訓練資料僅有約2萬多個數據點(data points),透過跨境共享的方式擴充至30萬個數據點。銀行在此情境中所採用機器學習方式為邏輯回歸(Logistic Regression),所需的資料欄位包含客戶所在位置郵遞區號(ZIP code)年消費金額與交易資料,用以算出客戶近期內會申請貸款之機率。運用之資料共享技術是結合全同態加密(Fully Homomorphic Encryption)以及安全多方計算,在Inpher的SaaS服務上以全同態加密方式進行運算,不同分行再透過安全多方計算輸入已加密後之資料。國內金融機構間的資料共享目前仍依循「金融機構間資料共享指引」進行,目前仍以使用者同意之前提發動資料共享,未來若資料共享指引還有進一步改版,此種資料共享技術或可列入應用之參考。
資料來源:
1.Yao, A. C. (1982). Protocols for secure computations. In 23rd annual symposium on foundations of computer science (sfcs 1982)(pp. 160-164). IEEE.
2.鍾勝民、何志良、丁川偉,「安全多方運算-確保使用者隱私的雲端「盲服務」」,電腦與通訊。2018/12/16。
3.Future of Financial Intelligence Sharing (Ed.)(January 8, 2021). Innovation and discussion paper: Case studies of the use of privacy preserving analysis to tackle financial crime.
封面圖
圖片來源:作者自行繪製
沒有留言:
張貼留言